4  Causal Steps, Confounding, and Causal Order

Comfort with [the principles of the basic mediation model] allows you to conduct mediation analysis and use it to shed light on your research questions and hypotheses about causal processes. In this chapter, [we] take up a variety of complications, including testing and ruling out various alternative explanations for associations observed in a mediation analysis, effect size, and models with multiple causal agents and outcomes. (Hayes, 2018, p. 113)

4.1 What about Barron and Kenny?

Complete and partial mediation are concepts that are deeply ingrained in the thinking of social and behavioral scientists. But I just don’t see what they offer our understanding of a phenomenon. They are too sample-size-dependent and the distinction between them has no substantive or theoretical meaning or value of any consequence. I recommend avoiding expressing hypotheses about mediation or results of a mediation analysis using these terms. (p. 121)

Agreed.

4.2 Confounding and causal order

One of the beautiful features of experiments is the causal interpretations they afford about differences between groups. Good experimentation is tough and requires lots of careful planning and strict control over experimental procedures, construction of stimuli, treatment of participants, and so forth. But when done well, no research design gives a researcher more confidence in the claim that differences between groups defined by \(X\) on some variable of interest is due to \(X\) rather than something else. Given that a mediation model is a causal model, the ability to make unequivocal causal claims about the effect of \(X\) on \(M\) and the direct and total effects of \(X\) on \(Y\) gives experiments tremendous appeal.

Absent random assignment to values of \(X\), all of the associations in a mediation model are susceptible to confounding and epiphenomenal association, not just the association between \(M\) and \(Y\). Whether one’s design includes manipulation and random assignment of \(X\) or not, it behooves the researcher to seriously ponder these potential threats to causal inference and, if possible, do something to reduce their plausibility as alternative explanations for associations observed. (pp. 121–122, emphasis in the original)

4.2.1 Accounting for confounding and epiphenomenal association

Here we load a couple necessary packages, load the data, and take a peek at them.

library(tidyverse)

estress <- read_csv("data/estress/estress.csv")

glimpse(estress)
Rows: 262
Columns: 7
$ tenure   <dbl> 1.67, 0.58, 0.58, 2.00, 5.00, 9.00, 0.00, 2.50, 0.50, 0.58, 9.00, 1.92, 2.00, 1.42, 0.92, 20.00, 2.00, 10.00, 0…
$ estress  <dbl> 6.0, 5.0, 5.5, 3.0, 4.5, 6.0, 5.5, 3.0, 5.5, 6.0, 5.5, 4.0, 3.0, 2.5, 3.5, 6.0, 4.0, 6.0, 3.5, 4.0, 2.5, 4.0, 2…
$ affect   <dbl> 2.60, 1.00, 2.40, 1.16, 1.00, 1.50, 1.00, 1.16, 1.33, 3.00, 3.00, 2.00, 1.83, 1.16, 1.16, 1.00, 1.33, 1.50, 1.3…
$ withdraw <dbl> 3.00, 1.00, 3.66, 4.66, 4.33, 3.00, 1.00, 1.00, 2.00, 4.00, 4.33, 1.00, 5.00, 1.66, 4.00, 1.33, 1.66, 1.66, 2.0…
$ sex      <dbl> 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, …
$ age      <dbl> 51, 45, 42, 50, 48, 48, 51, 47, 40, 43, 57, 36, 33, 29, 33, 48, 40, 45, 37, 42, 54, 57, 37, 49, 40, 30, 49, 31,…
$ ese      <dbl> 5.33, 6.05, 5.26, 4.35, 4.86, 5.05, 3.66, 6.13, 5.26, 4.00, 2.53, 6.60, 5.20, 5.66, 5.66, 5.40, 6.00, 6.13, 5.4…

As we learned in Section 2.3, the psych::lowerCor() function makes it easy to estimate the lower triangle of a correlation matrix.

psych::lowerCor(estress, digits = 3)
         tenur  estrs  affct  wthdr  sex    age    ese   
tenure    1.000                                          
estress   0.068  1.000                                   
affect   -0.065  0.340  1.000                            
withdraw -0.035  0.064  0.417  1.000                     
sex      -0.003  0.133  0.046  0.050  1.000              
age       0.266  0.066 -0.018 -0.035  0.083  1.000       
ese      -0.060 -0.158 -0.246 -0.243  0.028 -0.083  1.000

Let’s open brms.

library(brms)

Recall that if you want the correlations with Bayesian estimation and those sweet Bayesian credible intervals, you set up an intercept-only multivariate model.

model4.1 <- brm(
  data = estress, 
  family = gaussian,
  bf(mvbind(ese, estress, affect, withdraw) ~ 1) +
    set_rescor(TRUE),
  cores = 4,
  file = "fits/model04.01")

Behold the summary.

print(model4.1, digits = 3)
 Family: MV(gaussian, gaussian, gaussian, gaussian) 
  Links: mu = identity
         mu = identity
         mu = identity
         mu = identity 
Formula: ese ~ 1 
         estress ~ 1 
         affect ~ 1 
         withdraw ~ 1 
   Data: estress (Number of observations: 262) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Regression Coefficients:
                   Estimate Est.Error l-95% CI u-95% CI  Rhat Bulk_ESS Tail_ESS
ese_Intercept         5.609     0.059    5.492    5.724 1.000     6028     3177
estress_Intercept     4.619     0.089    4.446    4.792 1.000     6617     3425
affect_Intercept      1.597     0.045    1.507    1.685 1.000     4830     3362
withdraw_Intercept    2.319     0.077    2.168    2.467 1.000     5477     2881

Further Distributional Parameters:
               Estimate Est.Error l-95% CI u-95% CI  Rhat Bulk_ESS Tail_ESS
sigma_ese         0.953     0.042    0.876    1.040 1.003     7269     3259
sigma_estress     1.437     0.066    1.315    1.573 1.000     6874     3007
sigma_affect      0.729     0.033    0.669    0.796 1.001     5435     3052
sigma_withdraw    1.257     0.054    1.155    1.369 1.000     5319     3294

Residual Correlations: 
                         Estimate Est.Error l-95% CI u-95% CI  Rhat Bulk_ESS Tail_ESS
rescor(ese,estress)        -0.154     0.061   -0.270   -0.032 1.000     6116     3675
rescor(ese,affect)         -0.239     0.058   -0.350   -0.125 1.001     5302     3657
rescor(estress,affect)      0.335     0.056    0.222    0.441 1.001     4775     3127
rescor(ese,withdraw)       -0.237     0.058   -0.350   -0.127 0.999     5795     3309
rescor(estress,withdraw)    0.060     0.063   -0.062    0.183 1.004     5111     3440
rescor(affect,withdraw)     0.409     0.052    0.302    0.509 1.000     5508     3227

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Since we have posteriors for the correlations, why not plot them? Before we do, an asside: In previous editions of this book, we relied on the dark theme functions from the ggdark package (Grantham, 2019) for the plot themes. Though ggdark was formerly available on CRAN, it was removed on 2025-11-07 due to some unresolved issues (see here). There’s currently a promising looking pull request on GitHub that may fix the issue, but until the issue is resolved we’ll make substitutes by hand. Since I’m hoping this is a temporary fix, I’m not gong to explain the code in any detail.

dark_theme_gray <- function(...) {
  theme_gray(ink = "white", paper = "black", ...)
}

We’ll take our color scheme from the viridis package (Garnier, 2021).

as_draws_df(model4.1) %>% 
  pivot_longer(c(rescor__ese__estress, rescor__ese__affect, rescor__estress__withdraw)) %>% 
  
  ggplot(aes(x = value, fill = name)) +
  geom_density(alpha = 0.85, color = "transparent") +
  scale_fill_viridis_d(
    option = "D", direction = -1,
    labels = c(expression(rho["ese, affect"]),
               expression(rho["ese, estress"]),
               expression(rho["estress, withdraw"])),
    guide = guide_legend(label.hjust = 0,
                         label.theme = element_text(size = 15, angle = 0, color = "white"),
                         title.theme = element_blank())) +
  scale_x_continuous(NULL, limits = c(-1, 1)) +
  scale_y_continuous(NULL, breaks = NULL) +
  ggtitle("Our correlation density plot") +
  dark_theme_gray() +
  theme(panel.grid = element_blank())

In the last chapter, we said there were multiple ways to set up a multivariate model in brms. Our first approach was to externally define the submodels using the bf() function, save them as objects, and then include those objects within the brm() function. Another approach is to just define the separate bf() submodels directly in the brm() function, combining them with the + operator. That’s the approach we will practice in this chapter. Here’s what it looks like for our first mediation model.

model4.2 <- brm(
  data = estress, 
  family = gaussian,
  bf(withdraw ~ 1 + estress + affect + ese + sex + tenure) +
    bf(affect ~ 1 + estress + ese + sex + tenure) +
    set_rescor(FALSE),
  cores = 4,
  file = "fits/model04.02")

Worked like a charm. Here’s the summary.

print(model4.2, digits = 3)
 Family: MV(gaussian, gaussian) 
  Links: mu = identity
         mu = identity 
Formula: withdraw ~ 1 + estress + affect + ese + sex + tenure 
         affect ~ 1 + estress + ese + sex + tenure 
   Data: estress (Number of observations: 262) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Regression Coefficients:
                   Estimate Est.Error l-95% CI u-95% CI  Rhat Bulk_ESS Tail_ESS
withdraw_Intercept    2.750     0.563    1.613    3.868 1.000     6500     3084
affect_Intercept      1.786     0.308    1.169    2.399 1.000     6773     2454
withdraw_estress     -0.094     0.054   -0.199    0.010 1.001     7234     3453
withdraw_affect       0.706     0.107    0.503    0.917 1.000     6337     3025
withdraw_ese         -0.213     0.079   -0.368   -0.058 1.000     6842     3026
withdraw_sex          0.127     0.142   -0.153    0.405 1.001     8407     3396
withdraw_tenure      -0.002     0.011   -0.023    0.019 1.000     7936     3084
affect_estress        0.160     0.030    0.100    0.219 1.000     7253     3035
affect_ese           -0.155     0.044   -0.241   -0.069 1.003     6948     2874
affect_sex            0.015     0.087   -0.154    0.188 1.001     6453     2509
affect_tenure        -0.011     0.006   -0.024    0.002 1.002     9396     3026

Further Distributional Parameters:
               Estimate Est.Error l-95% CI u-95% CI  Rhat Bulk_ESS Tail_ESS
sigma_withdraw    1.126     0.050    1.030    1.228 1.002     7282     3142
sigma_affect      0.671     0.030    0.616    0.732 1.003     7712     3091

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

In the printout, notice how first within intercepts and then with covariates and sigma, the coefficients are presented as for withdraw first and then affect. Also notice how the coefficients for the covariates are presented in the same order for each criterion variable. Hopefully that’ll make it easier to sift through the printout. Happily, our coefficients are quite similar to those in Table 4.1.

Here are the \(R^2\) summaries.

bayes_R2(model4.2) %>% round(digits = 3)
           Estimate Est.Error  Q2.5 Q97.5
R2withdraw    0.213     0.040 0.136 0.289
R2affect      0.171     0.037 0.099 0.244

These are also in the same ballpark, but a little higher. Why not glance at their densities?

bayes_R2(model4.2, summary = F) %>% 
  data.frame() %>% 
  pivot_longer(everything()) %>% 
  
  ggplot(aes(x = value, fill = name)) +
  geom_density(color = "transparent", alpha = 0.85) +
  scale_fill_viridis_d(option = "A", begin = 0.33, direction = -1,
                       labels = c("affect", "withdaw"),
                       guide  = guide_legend(title.theme = element_blank())) +
  scale_x_continuous(NULL, limits = 0:1) +
  scale_y_continuous(NULL, breaks = NULL) +
  ggtitle(expression(The~italic(R)^2~distributions~"for"~model~4.2)) +
  dark_theme_gray() +
  theme(panel.grid = element_blank())

Here we retrieve the posterior samples, compute the indirect effect, and summarize the indirect effect with quantile().

draws <- as_draws_df(model4.2) %>% 
  mutate(ab = b_affect_estress * b_withdraw_affect)

quantile(draws$ab, probs = c(0.5, 0.025, 0.975)) %>% 
  round(digits = 3)
  50%  2.5% 97.5% 
0.111 0.064 0.170

The results are similar to those in the text (p. 127). Here’s what it looks like.

draws %>% 
  ggplot(aes(x = ab)) +
  geom_density(aes(fill = factor(0)),
               color = "transparent", show.legend = F) +
  geom_vline(xintercept = quantile(draws$ab, probs = c(0.5, 0.025, 0.975)),
             color = "black", linetype = c(1, 3, 3)) +
  scale_fill_viridis_d(option = "A", begin = 0.6) +
  scale_y_continuous(NULL, breaks = NULL) +
  xlab(expression(italic(ab))) +
  dark_theme_gray() +
  theme(panel.grid = element_blank())

Once again, those sweet Bayesian credible intervals get the job done.

Here’s a way to get both the direct effect, \(c'\) (i.e., b_withdraw_estress), and the total effect, \(c\) (i.e., \(c'\) + \(ab\)) of estress on withdraw.

draws %>% 
  mutate(c       = b_withdraw_estress + ab,
         c_prime = b_withdraw_estress) %>% 
  pivot_longer(c(c_prime, c)) %>% 
  group_by(name) %>% 
  summarize(mean = mean(value), 
            ll   = quantile(value, probs = 0.025),
            ul   = quantile(value, probs = 0.975)) %>% 
  mutate_if(is_double, round, digits = 3)
# A tibble: 2 × 4
  name      mean     ll    ul
  <chr>    <dbl>  <dbl> <dbl>
1 c        0.019 -0.091  0.13
2 c_prime -0.094 -0.199  0.01

Both appear pretty small. Which leads us to the next section…

4.3 Effect size

The quantification of effect size in mediation analysis is an evolving area of thought and research. [Hayes described] two measures of effect size that apply to the direct, indirect, and total effects in a mediation model…. For an excellent discussion of measures of effect size in mediation analysis, see Preacher and Kelley (2011). [We will] use their notation below. (p. 133)

4.3.1 The partially standardized effect

We get \(\textit{SD}\)’s using the sd() function. Here’s the \(\textit{SD}\) for our \(Y\) variable, withdraw.

sd(estress$withdraw)
[1] 1.24687

Here we compute the partially standardized effect sizes for \(c'\) and \(ab\) by dividing those vectors in our post object by sd(estress$withdraw), which we saved as sd_y.

sd_y <- sd(estress$withdraw)

draws %>% 
  mutate(c_prime_ps = b_withdraw_estress / sd_y,
         ab_ps      = ab / sd_y) %>% 
  mutate(c_ps = c_prime_ps + ab_ps) %>% 
  pivot_longer(c(c_prime_ps, ab_ps, c_ps)) %>% 
  group_by(name) %>% 
  summarize(mean   = mean(value), 
            median = median(value),
            ll     = quantile(value, probs = 0.025),
            ul     = quantile(value, probs = 0.975)) %>% 
  mutate_if(is_double, round, digits = 3)
# A tibble: 3 × 5
  name         mean median     ll    ul
  <chr>       <dbl>  <dbl>  <dbl> <dbl>
1 ab_ps       0.09   0.089  0.051 0.136
2 c_prime_ps -0.075 -0.075 -0.16  0.008
3 c_ps        0.015  0.015 -0.073 0.104

The results are similar, though not identical, to those in the text. Here we have both rounding error and estimation differences at play. The plots:

 draws %>% 
  mutate(c_prime_ps = b_withdraw_estress / sd_y,
         ab_ps      = ab / sd_y) %>% 
  mutate(c_ps = c_prime_ps + ab_ps) %>% 
  pivot_longer(c(c_prime_ps, ab_ps, c_ps)) %>% 

  ggplot(aes(x = value, fill = name)) +
  geom_density(alpha = 0.85, color = "transparent") +
  scale_fill_viridis_d(option = "D", breaks = NULL) +
  scale_y_continuous(NULL, breaks = NULL) +
  labs(title = "Partially-standardized coefficients",
       x = NULL) +
  dark_theme_gray() +
  theme(panel.grid = element_blank()) +
  facet_wrap(~ name, ncol = 3)

On page 135, Hayes revisited the model from Section 3.3. We’ll have to reload the data and refit that model to follow along. First, load the data.

pmi <- read_csv("data/pmi/pmi.csv")

Refit the model, this time with the bf() statements defined right within brm().

model4.3 <- brm(
  data = pmi, 
  family = gaussian,
  bf(reaction ~ 1 + pmi + cond) + 
    bf(pmi ~ 1 + cond) + 
    set_rescor(FALSE),
  cores = 4,
  file = "fits/model04.03")

The partially-standardized parameters require some as_draws_df() wrangling.

draws <- as_draws_df(model4.3)

sd_y <- sd(pmi$reaction)

draws %>% 
  mutate(ab      = b_pmi_cond * b_reaction_pmi,
         c_prime = b_reaction_cond) %>% 
  mutate(ab_ps      = ab / sd_y,
         c_prime_ps = c_prime / sd_y) %>% 
  mutate(c_ps = c_prime_ps + ab_ps) %>% 
  pivot_longer(c(c_prime_ps, ab_ps, c_ps)) %>%
  group_by(name) %>% 
  summarize(mean   = mean(value), 
            median = median(value),
            ll     = quantile(value, probs = 0.025),
            ul     = quantile(value, probs = 0.975)) %>% 
  mutate_if(is_double, round, digits = 3)
# A tibble: 3 × 5
  name        mean median     ll    ul
  <chr>      <dbl>  <dbl>  <dbl> <dbl>
1 ab_ps      0.156  0.151  0     0.338
2 c_prime_ps 0.161  0.16  -0.17  0.504
3 c_ps       0.317  0.319 -0.047 0.686

Happily, these results are closer to those in the text than with the previous example.

4.3.2 The completely standardized effect

Note. Hayes could have made this clearer in the text, but the estress model he referred to in this section was the one from way back in Section 3.5, not the one from earlier in this chapter.

One way to get a standardized solution is to standardize the variables in the data and then fit the model with those standardized variables. To do so, we’ll revisit our custom standardize(), put it to work, and fit the standardized version of the model from Section 3.5, which we’ll call model4.4.

# make the function
standardize <- function(x) {
  (x - mean(x)) / sd(x)
}

# use the function
estress <- estress %>% 
  mutate(withdraw_z = standardize(withdraw), 
         estress_z  = standardize(estress), 
         affect_z   = standardize(affect))

Fit the model.

model4.4 <- brm(
  data = estress, 
  family = gaussian,
  bf(withdraw_z ~ 1 + estress_z + affect_z) + 
    bf(affect_z ~ 1 + estress_z) + 
    set_rescor(FALSE),
  cores = 4,
  file = "fits/model04.04")

Here they are, our newly standardized coefficients.

fixef(model4.4) %>% round(digits = 3)
                    Estimate Est.Error   Q2.5 Q97.5
withdrawz_Intercept    0.000     0.057 -0.113 0.113
affectz_Intercept      0.001     0.059 -0.115 0.118
withdrawz_estress_z   -0.088     0.058 -0.199 0.029
withdrawz_affect_z     0.446     0.060  0.327 0.568
affectz_estress_z      0.340     0.058  0.228 0.458

Here we do the wrangling necessary to spell out the standardized effects for \(ab\), \(c'\), and \(c\).

as_draws_df(model4.4) %>% 
  mutate(ab_s      = b_affectz_estress_z * b_withdrawz_affect_z,
         c_prime_s = b_withdrawz_estress_z) %>%
  mutate(c_s = ab_s + c_prime_s) %>% 
  pivot_longer(c(c_prime_s, ab_s, c_s)) %>%
  group_by(name) %>% 
  summarize(mean   = mean(value), 
            median = median(value),
            ll     = quantile(value, probs = 0.025),
            ul     = quantile(value, probs = 0.975)) %>% 
  mutate_if(is_double, round, digits = 3)
# A tibble: 3 × 5
  name        mean median     ll    ul
  <chr>      <dbl>  <dbl>  <dbl> <dbl>
1 ab_s       0.152  0.15   0.093 0.221
2 c_prime_s -0.088 -0.089 -0.199 0.029
3 c_s        0.064  0.064 -0.055 0.183

Let’s confirm that we can recover these values by applying the formulas on page 135 to the unstandardized model, which we’ll call model4.5. First, we’ll have to fit that model since we haven’t fit that one since Chapter 3.

model4.5 <- brm(
  data = estress, 
  family = gaussian,
  bf(withdraw ~ 1 + estress + affect) + 
    bf(affect ~ 1 + estress) + 
    set_rescor(FALSE),
  cores = 4,
  file = "fits/model04.05")

Check the unstandardized coefficient summaries.

fixef(model4.5) %>% round(digits = 3)
                   Estimate Est.Error   Q2.5 Q97.5
withdraw_Intercept    1.445     0.256  0.928 1.943
affect_Intercept      0.800     0.142  0.520 1.080
withdraw_estress     -0.076     0.054 -0.181 0.029
withdraw_affect       0.768     0.104  0.565 0.965
affect_estress        0.173     0.030  0.114 0.232

On pages 135–136, Hayes provided the formulas to compute the standardized effects, which are

\[ \begin{align*} c'_{cs} & = \frac{\textit{SD}_X(c')}{\textit{SD}_{Y}} = \textit{SD}_{X}(c'_{ps}), \\ ab_{cs} & = \frac{\textit{SD}_X(ab)}{\textit{SD}_{Y}} = \textit{SD}_{X}(ab_{ps}), \text{and} \\ c_{cs} & = \frac{\textit{SD}_X(c)}{\textit{SD}_{Y}} = c'_{cs} + ab_{ps}, \end{align*} \] where the \(ps\) subscript indicates partially standardized. Here we put them in action to standardize the unstandardized results.

sd_x <- sd(estress$estress)
sd_y <- sd(estress$withdraw)

as_draws_df(model4.5) %>% 
  mutate(ab      = b_affect_estress * b_withdraw_affect,
         c_prime = b_withdraw_estress) %>% 
  mutate(ab_s      = (sd_x * ab) / sd_y,
         c_prime_s = (sd_x * c_prime) / sd_y) %>% 
  mutate(c_s = ab_s + c_prime_s) %>% 
  pivot_longer(c(c_prime_s, ab_s, c_s)) %>%
  group_by(name) %>% 
  summarize(mean   = mean(value), 
            median = median(value),
            ll     = quantile(value, probs = 0.025),
            ul     = quantile(value, probs = 0.975)) %>% 
  mutate_if(is_double, round, digits = 3)
# A tibble: 3 × 5
  name        mean median     ll    ul
  <chr>      <dbl>  <dbl>  <dbl> <dbl>
1 ab_s       0.152  0.151  0.091 0.224
2 c_prime_s -0.087 -0.087 -0.207 0.033
3 c_s        0.065  0.065 -0.058 0.192

Success!

4.3.3 Some (problematic) measures only for indirect effects

Hayes recommended against these, so I’m not going to bother working any examples.

4.4 Statistical power

As Hayes discussed, power is an important but thorny issue within the frequentist paradigm. Given that we’re not particularly interested in rejecting the point-null hypothesis as Bayesians and that we bring in priors (which we’ve largely avoided explicitly mentioning in his project but have been quietly using all along), the issue is even more difficult for Bayesians. To learn more on the topic, check out Chapter 13 in Kruschke’s (2015) text; Miočević, MacKinnon, and Levy’s (2017) paper on power in small-sample Bayesian analyses; or Gelman and Carlin’s (2014) paper offering an alternative to the power paradigm. You might look at Matti Vuorre’s Sample size planning with brms project. And finally, I have a series of blog posts on Bayesian power analyses. You can find the first post here.

4.5 Multiple \(X\)s or \(Y\)s: Analyze separately or simultaneously?

“Researchers sometimes propose that several causal agents (\(X\) variables simultaneously transmit their effects on the same outcome through the same mediator(s)” (p. 141).

4.5.1 Multiple \(X\) variables

The danger in including multiple \(X\)’s in a mediation model, as when including statistical controls, is the possibility that highly correlated \(X\)s will cancel out each other’s effects. This is a standard concern in linear models involving correlated predictors. Two \(X\) variables (or an \(X\) variable and a control variable) highly correlated with each other may also both be correlated with \(M\) or \(Y\), so when they are both included as predictors of \(M\) or \(Y\) in a mediation model, they compete against each other in their attempt to explain variation in \(M\) and \(Y\). Their regression coefficients quantify their unique association with the model’s mediator and outcome variable(s). at the extreme, the two variables end up performing like two boxers in the ring simultaneously throwing a winning blow at the other at precisely the same time. Both get knocked out and neither goes away appearing worthy of a prize. The stronger the associations between the variables in the model, the greater the potential of such a problem. (pp. 143–144)

The same basic problems with multicollinearity applies to the Bayesian paradigm, too.

4.5.2 Estimation of a model with multiple \(X\) variables in PROCESS brms

Hayes discussed the limitation that his PROCESS program may only handle a single \(X\) variable in the x= part of the command line, for which he displayed a workaround. We don’t have such a limitation in brms. Using Hayes’s hypothetical data syntax for a model with three \(X\)’s, the brms code would look like this.

model4.6 <- brm(
  data = data, 
  family = gaussian,
  bf(dv ~ 1 + iv1 + iv2 + iv3 + med) + 
    bf(med ~ 1 + iv1 + iv2 + iv3) + 
    set_rescor(FALSE),
  cores = 4)

To show it in action, let’s simulate some data.

n <- 1e3

set.seed(4.5)
d <- tibble(
  iv1 = rnorm(n, mean = 0, sd = 1),
  iv2 = rnorm(n, mean = 0, sd = 1),
  iv3 = rnorm(n, mean = 0, sd = 1)) %>% 
  mutate(med = rnorm(n, mean = 0 + iv1 * -1 + iv2 * 0 + iv3 * 1, sd = 1),
         dv  = rnorm(n, mean = 0 + iv1 * 0 + iv2 * .5 + iv3 * 1 + med * .5, sd = 1))

head(d)
# A tibble: 6 × 5
     iv1    iv2     iv3    med     dv
   <dbl>  <dbl>   <dbl>  <dbl>  <dbl>
1  0.217  0.177 -1.39   -0.755 -1.77 
2 -0.542  1.69   0.0513  0.721  0.402
3  0.891 -1.35   1.10    0.777 -0.132
4  0.596  1.08  -0.203  -0.955  1.02 
5  1.64  -0.456 -0.428  -2.89  -3.26 
6  0.689 -0.681 -0.429  -0.462 -2.38

Before we proceed, if data simulation is new to you, you might check out Roger Peng’s helpful tutorial or this great post by Ariel Muldoon.

Here we fit the model.

model4.6 <- brm(
  data = d, 
  family = gaussian,
  bf(dv ~ 1 + iv1 + iv2 + iv3 + med) + 
    bf(med ~ 1 + iv1 + iv2 + iv3) + 
    set_rescor(FALSE),
  cores = 4,
  file = "fits/model04.06")

Behold the results.

print(model4.6)
 Family: MV(gaussian, gaussian) 
  Links: mu = identity
         mu = identity 
Formula: dv ~ 1 + iv1 + iv2 + iv3 + med 
         med ~ 1 + iv1 + iv2 + iv3 
   Data: d (Number of observations: 1000) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Regression Coefficients:
              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
dv_Intercept     -0.01      0.03    -0.07     0.05 1.00     5819     2834
med_Intercept     0.00      0.03    -0.06     0.06 1.00     5669     2892
dv_iv1            0.02      0.04    -0.06     0.11 1.00     3309     3276
dv_iv2            0.56      0.03     0.50     0.63 1.00     5713     3454
dv_iv3            1.01      0.05     0.92     1.10 1.00     2585     2738
dv_med            0.46      0.03     0.40     0.53 1.00     2542     2807
med_iv1          -0.93      0.03    -1.00    -0.87 1.00     5888     2839
med_iv2           0.03      0.03    -0.03     0.09 1.00     5719     2992
med_iv3           0.98      0.03     0.92     1.04 1.00     5590     2976

Further Distributional Parameters:
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma_dv      1.00      0.02     0.96     1.05 1.00     5307     3205
sigma_med     0.97      0.02     0.93     1.02 1.00     5562     3035

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Good old brms::brm() came through just fine. If you wanted to simulate data with a particular correlation structure for the iv variables, you might use the mvnorm() function from the MASS package (Ripley, 2022), about which you might learn more here.

4.5.3 Multiple \(Y\) variables.

We’ve already been using the multivariate syntax in brms for our simple mediation models. Fitting a mediation model with multiple \(Y\) variables is a minor extension. To see, let’s simulate more data.

n <- 1e3

set.seed(4.5)
d <- tibble(iv = rnorm(n, mean = 0, sd = 1)) %>% 
  mutate(med = rnorm(n, mean = 0 + iv * .5, sd = 1)) %>% 
  mutate(dv1 = rnorm(n, mean = 0 + iv * -1 + med * 0,  sd = 1),
         dv2 = rnorm(n, mean = 0 + iv * 0  + med * .5, sd = 1),
         dv3 = rnorm(n, mean = 0 + iv * 1  + med * 1,  sd = 1))

head(d)
# A tibble: 6 × 5
      iv    med    dv1    dv2     dv3
   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>
1  0.217  0.285 -1.61   0.999  0.420 
2 -0.542  1.42   0.594  0.836  0.0208
3  0.891 -0.902  0.206  0.120 -0.954 
4  0.596  1.37  -0.799  0.530  3.13  
5  1.64   0.362 -2.06  -0.643  0.840 
6  0.689 -0.337 -1.12   0.487 -1.03

Fitting this model requires a slew of bf() statements.

model4.7 <- brm(
  data = d, 
  family = gaussian,
  bf(dv1 ~ 1 + iv + med) + 
    bf(dv2 ~ 1 + iv + med) + 
    bf(dv3 ~ 1 + iv + med) + 
    bf(med ~ 1 + iv) + 
    set_rescor(FALSE),
  cores = 4,
  file = "fits/model04.07")
print(model4.7)
 Family: MV(gaussian, gaussian, gaussian, gaussian) 
  Links: mu = identity
         mu = identity
         mu = identity
         mu = identity 
Formula: dv1 ~ 1 + iv + med 
         dv2 ~ 1 + iv + med 
         dv3 ~ 1 + iv + med 
         med ~ 1 + iv 
   Data: d (Number of observations: 1000) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Regression Coefficients:
              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
dv1_Intercept     0.01      0.03    -0.05     0.07 1.00     8446     3124
dv2_Intercept     0.00      0.03    -0.06     0.06 1.00     9440     3088
dv3_Intercept    -0.01      0.03    -0.07     0.05 1.00     8834     2679
med_Intercept     0.03      0.03    -0.04     0.09 1.00     8037     3025
dv1_iv           -1.05      0.04    -1.12    -0.98 1.00     7287     3338
dv1_med           0.05      0.03    -0.01     0.11 1.00     7047     3141
dv2_iv            0.05      0.04    -0.02     0.12 1.00     6451     3614
dv2_med           0.53      0.03     0.47     0.59 1.00     6383     3468
dv3_iv            1.03      0.04     0.96     1.10 1.00     6401     3540
dv3_med           1.06      0.03     1.00     1.12 1.00     6662     2518
med_iv            0.53      0.03     0.46     0.59 1.00     9683     2862

Further Distributional Parameters:
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma_dv1     0.98      0.02     0.93     1.02 1.00     9324     2977
sigma_dv2     0.97      0.02     0.93     1.02 1.00     8685     3020
sigma_dv3     1.00      0.02     0.96     1.05 1.00     9268     3234
sigma_med     1.00      0.02     0.96     1.04 1.00     9201     2642

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Once again, brms to the rescue!

4.6 Chapter summary

Statistical mediation analysis has changed since the publication of Baron and Kenny (1986). The heyday of the causal steps “criteria to establish mediation” approach is over. Also disappearing in the 21 century is a concern about whether a process can be labeled as complete or partial mediation. Modern mediation analysis emphasizes an explicit estimation of the indirect effect, inferential tests of the indirect effect that don’t make unnecessary assumptions, and an acknowledgement that evidence of a statistically significant association between \(X\) and \(Y\) is not necessary to talk about a model intervening variable process (in which case the concepts of complete and partial mediation simply don’t make sense). (p. 146)

To this, I’ll just point out Hayes is speaking from a frequentist hypothesis-testing orientation. If you would like to dwell on significance tests, you certainty can. But particularly from within the Bayesian paradigm, you just don’t need to.

Session info

sessionInfo()
R version 4.5.1 (2025-06-13)
Platform: aarch64-apple-darwin20
Running under: macOS Ventura 13.4

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/Chicago
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] brms_2.23.0     Rcpp_1.1.0      lubridate_1.9.4 forcats_1.0.1   stringr_1.6.0   dplyr_1.1.4     purrr_1.2.1    
 [8] readr_2.1.5     tidyr_1.3.2     tibble_3.3.1    ggplot2_4.0.1   tidyverse_2.0.0

loaded via a namespace (and not attached):
 [1] tidyselect_1.2.1        psych_2.5.6             viridisLite_0.4.2       farver_2.1.2            loo_2.9.0.9000         
 [6] S7_0.2.1                fastmap_1.2.0           TH.data_1.1-4           tensorA_0.36.2.1        digest_0.6.39          
[11] timechange_0.3.0        estimability_1.5.1      lifecycle_1.0.5         StanHeaders_2.36.0.9000 survival_3.8-3         
[16] magrittr_2.0.4          posterior_1.6.1.9000    compiler_4.5.1          rlang_1.1.7             tools_4.5.1            
[21] utf8_1.2.6              yaml_2.3.12             knitr_1.51              labeling_0.4.3          bridgesampling_1.2-1   
[26] htmlwidgets_1.6.4       curl_7.0.0              bit_4.6.0               pkgbuild_1.4.8          mnormt_2.1.1           
[31] plyr_1.8.9              RColorBrewer_1.1-3      abind_1.4-8             multcomp_1.4-29         withr_3.0.2            
[36] grid_4.5.1              stats4_4.5.1            xtable_1.8-4            inline_0.3.21           emmeans_1.11.2-8       
[41] scales_1.4.0            MASS_7.3-65             cli_3.6.5               mvtnorm_1.3-3           rmarkdown_2.30         
[46] crayon_1.5.3            generics_0.1.4          RcppParallel_5.1.11-1   rstudioapi_0.17.1       reshape2_1.4.5         
[51] tzdb_0.5.0              rstan_2.36.0.9000       splines_4.5.1           bayesplot_1.15.0.9000   parallel_4.5.1         
[56] matrixStats_1.5.0       vctrs_0.7.0             V8_8.0.1                Matrix_1.7-3            sandwich_3.1-1         
[61] jsonlite_2.0.0          hms_1.1.4               bit64_4.6.0-1           glue_1.8.0              codetools_0.2-20       
[66] distributional_0.5.0    stringi_1.8.7           gtable_0.3.6            QuickJSR_1.8.1          pillar_1.11.1          
[71] htmltools_0.5.9         Brobdingnag_1.2-9       R6_2.6.1                vroom_1.6.6             evaluate_1.0.5         
[76] lattice_0.22-7          backports_1.5.0         rstantools_2.5.0.9000   gridExtra_2.3           coda_0.19-4.1          
[81] nlme_3.1-168            checkmate_2.3.3         xfun_0.55               zoo_1.8-14              pkgconfig_2.0.3

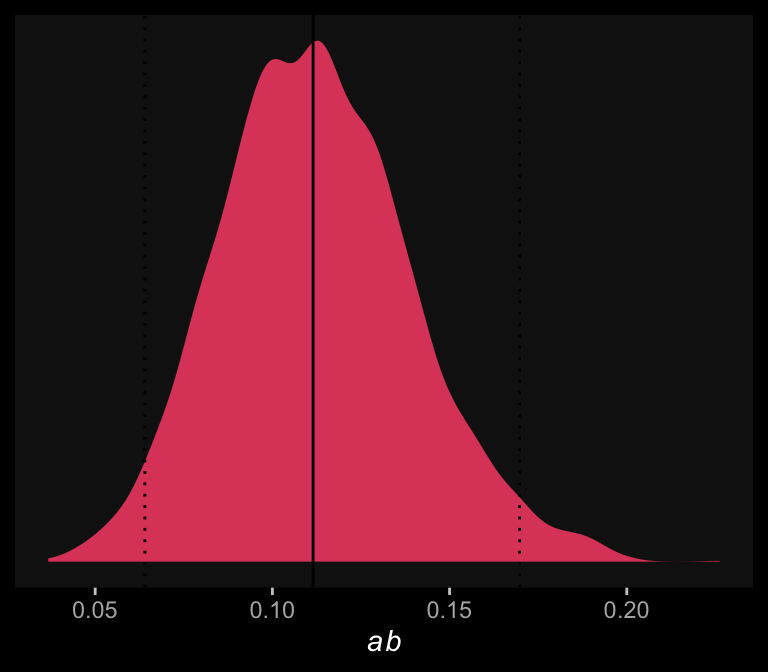
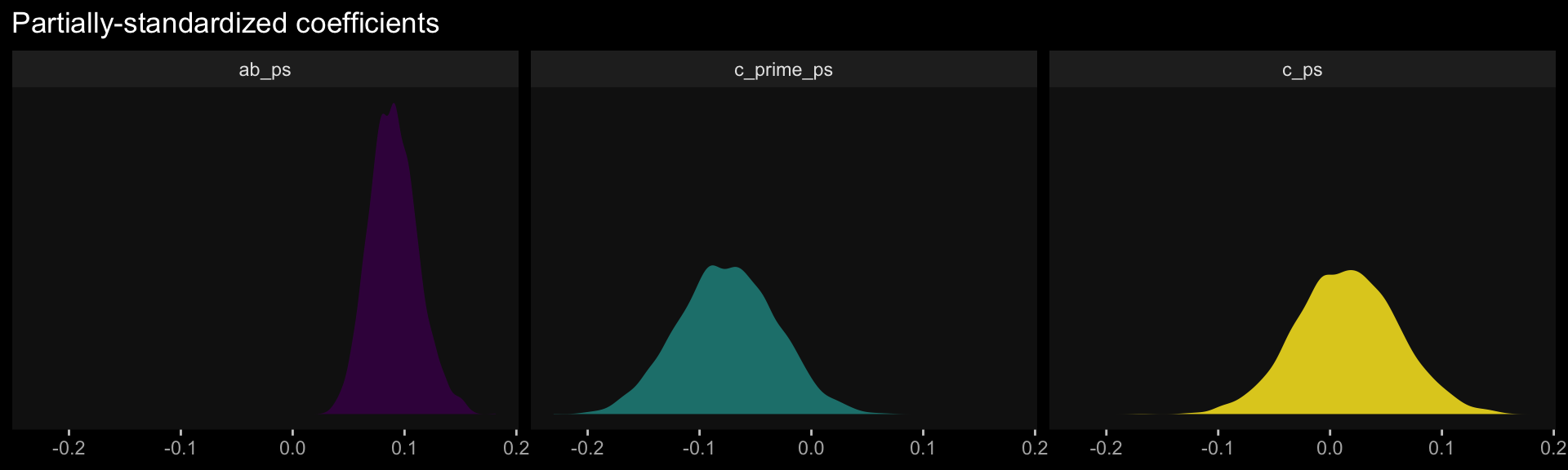
Comments